Определение допустимой интенсивности вылова с учетом общих закономерностей убыли поколения промыслового стада

Для приближенной оценки допустимой интенсивности при при достаточно уравновешенном состоянии запаса и промысла можно воспользоваться общими закономерностями убыли поколения промыслового стада с учетом постоянной и не зависящей от возраста промысловой и естественной смертности.

Запишем выражение для оценки рассматриваемой убыли поколения от величины пополнения промыслового стада R до практически полного его исчезновения в предельном возрасте tп:

(4.23)

tR - возраст вступления рыбы в промысловое стадо; F и M - соответственно коэффициенты промысловой и естественной смертности в возрасте от tR до tп ; Ntп- численность популяции в возрасте tп.

Из уравнения (4.23) можно получить выражение для оценки допустимого коэффициента промысловой смертности при заданной начальной и конечной численности популяции:

ln(Ntп /R)

[F] =————— - M. (4.24)

tп - tR

Выражение (4.24) можно преобразовать с учетом того, что числитель выражения ln(Ntп /R) - величина, которая при небольших реальных значениях Ntп /R близка к (- 4,6). С учетом этого уравнение (4.24) можно переписать в следующем виде:

4,6

[F] = ——— - M. (9.25)

tп – tR

Кроме того, известно эмпирическое выражение для оценки коэффициента естественной смертности вида М = а1 / (tпр - tп). С учетом последнего выражения формула (4.24) для оценки допустимого коэффициента промысловой смертности примет вид:

2,4

[F] = ———. (4.26)

tп - tR

Выражение (4.26) можно переписать также в следующем виде, более удобном для решения некоторых задач:

2,4

[F] = ——————. (4.27)

tп (1 - tR/tп)

Рис 4.2 График для оценки допустимого коэффициента промысловой смертности

С применением выражений (4.26) и (4.27) несложно определять допустимую интенсивность вылова с учетом известного коэффициента естественной смертности.

Следует обратить внимание, что при использовании рассматриваемого способа отношение допустимого коэффициента промысловой смертности к коэффициенту естественной смертности при любом предельном возрасте рыбы одинаково и близко к 1,1. Величина полученного отношения близка к значению аналогичного отношения, которое из других соображений получил П.В. Тюрин (1962).

Предложен сходный с рассмотренным способ определения допустимой промысловой смертности рыб, в котором принято несколько иное (экспоненциальное) выражение М = - ln (1 - e-0,13 tпр) для определения не зависящего от возраста значения коэффициента естественной смертности (выражение справедливо для tп= 4 - 15 лет).

С учетом этой формулы получим новое выражение для определения допустимого коэффициента промысловой смертности, считая,как и раньше, значение Ntп /R небольшим, а ln(Ntп /R) = - 4,6.

4,6 - 0,1 tп

[F] = ————— - е. (9.28)

tп - tR

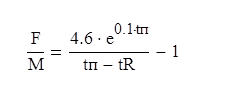С учетом этих выражений получим отношение:

Зависимость F/M от tп наглядно показана на рис 4.3

Рис 4.3 Зависимость F/M от tп

В рассмотренном способе оценки допустимой интенсивности вылова в расчет обычно принимают возраст, соответствующий наиболее взрослым рыбам в промысловом стаде. Кроме того, возможен расчетный случай, когда предельный возраст рыбы задают из некоторых соображений меньше предельного с учетом "нормальной" интенсивности вылова, как, например, при необходимости увеличения коэффициента использования биомассы поколения или улова на единицу пополнения промыслового стада.

Популярные статьи:

Потенциал-активируемые натриевые каналы
Методы, которые были использованы для характеристики молекулярной структуры АХР, были также успешно применены к потенциал-активируемым каналам. Ключевыми шагами в этом процессе были биохимическая экстракция и изоляция протеина с последующ ...

Грудина и ребра
Грудиной называется длинная губчатая кость плоской формы, замыкающая грудную клетку спереди. В строении грудины выделяют три части: тело грудины, рукоятку грудины и мечевидный отросток, которые с возрастом (обычно к 30–35 годам) срастаютс ...

Здоровье человека, определение, многогранность форм его проявления (обзор литературы)
Понятие «Здоровье человека», на первый взгляд, представляется простым и ясным. Здоровый человек вообще не задумывается над смыслом этого состояния. Не случайно Ф.Энгельс в своё время сделал очень простое определение здоровья: «Здоровье – ...